You guys should talk...

http://www.lotustalk.com/forums/f3/selecting-setting-springs-shocks-sway-bars-73703/

 

Really you need the slope of the upper and lower control arm and perpendicular distance from there pivot point to there corresponding ball joint.

 

Hey try this

It work as long as all units are consistant

 

screen

 

For lowering/ raising the vehicle just add/ subtract that amount to the two body points and the sheet should do the rest

 

This is great.

What exactly are we measuring with the M line 1/M line 2/ and y2?

I don't really understand the position result. The position should be in the centerline and not change (assuming the car is flat and ride height are equal on both sides)

 

M1, M2 slopes of the lines
y2 is y intercept of the UCA, I made y1 go thru the origin. You really don’t’ need them there just an interim to get to the final answer.

Position is just the distance from underneath the ball joint to the intersection of the UCA LCA arm vectors. Tells you if its converges away from or towards the center of the car.

 

I cleaned up the sheet a little more

 

To calculate the roll center, don't we need to measure the point where the "virtual" control arms meet, and then draw a line from that point to the center of the tire contact patch?

The roll center height where that line is in the center axis of the car.

I don't see how you can calculate it without knowing the hub measurements, rim width and rim offset.

Maybe I am missing something here.

 

THe roll center would be the purple dot

The point in the middle of the car where the line from the center line of the tire converges with the line you calculated.

 

forgot the pic

 

actually, I don't think we need to know the wheel measurements and hub measurements, we just need to calculate it based on the track.

The front track is 1457 mm / 57.4 in and the rear track is 1503 mm / 59.2 in. This may change with different wheel setups but would be easy to calculate.

 

You just need the ball joint locations and the arm mounting points to the body to get the slope. For the centers height and location from the joint and add in half the tire width and you can get the radius (yellow line). There are some other methods but this will work for instantaneous centers.

 

It's nice to be able to see what the roll center does as the car moves up and down and rolls side to side on its suspension.

 

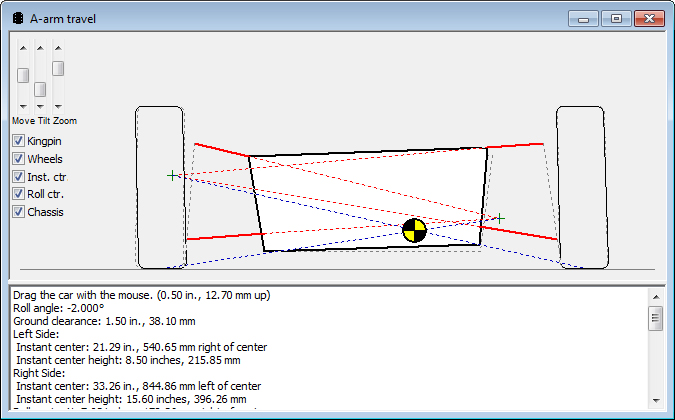
FWIW, this is a very simple exercise to do in a 3D modeling program such as Solidworks. No need for expensive suspension modeling software if all you want to find is roll center migration.

Just draw a 2D sketch and make the control arm, track, and hub geometry constant. Then change the ride height or the roll angle. All of the proper constraints are pretty intuitive once you get down to thinking about it.

If you have a kinematics toolbox like CATIA does, generating graphs of RC migration or camber are just one more step away.

Of course knowing the RC migration isn't very helpful without a fairly good guess at the CG location. That is the key to most of the usefulness From there you can even start solving for loads in any suspension member or bushing with almost no more work.

 

Just fixed it, now it will give you the roll center your looking for

 

Thanks! That is great.

I will try to get the measurements and positions of the control arms next week when I get the car on a hoist.

One thing though, if one control arm is completely horizontal, the M line is 0 and then it cant calulate anything. I'm not sure why, but it must be possible in some cases to have a completely horizontal control arm.

 

Yes in that case the height is zero because those lines never intersect. So if the spreadsheet ever comes up with an error than it's zero. I'd have to put in a descent amount of logic for that

Also be careful measuring on a hoist if the wheels move poistion would change some values

 

No, if one control arm in completely horizontal the lines should still cross. They would only not cross if both control arms are horizontal which would not happen.

IN this formula, if either control arm is horizontal it gives an error, so something seems wrong.

In your diagram, the lower arm is completely horizontal and all the lines cross and the roll center is not zero.

 

Sorry I misunderstood, I thought you meant both horizontal. let me work on that, it shouldn't be hard to fix

 

Ok try it now

 

I'm taking my measurements of this. Where would be the proper place to measure the knuckle ball joint height? The point where the knuckle bolts to the knuckle or the center of the balljoint on the a-arm?

 

The pivot point is what's important, which is probably about the center of the joint.

 

I made a mistake in the logic try this update. I'm going to run the calculation manually

 

I believe there is still an error in the formula. In this formula, the roll center is higher off the ground as the car gets lower (distance to the control arm pivots shortens).

So, something does not seem right.

 

Didn't someone say this is an extremely simple calculation?

rotflrotflrotflrotflrotflrotfl

It's not. Especially if it needs to work with any suspension, symmetrical or not. It took us thousands of lines of C++ code and many months to perfect it in Speed-Wiz.

 

I personally believe just the roll center it straight forward. It's a couple of lines intersecting. Although I have had to revise it like 6 times. rotfl

I do believe its functional now

 

OK so the spreadsheet did have a small error. I fixed it and even graphed several examples to check and it looks fine with the new rev. Even still as you lower the car the roll center gets higher, and that’s because the lower control arm is already pointing up so as you lower the car more it points even higher by the time the line projected intersects that the intersection point gets higher. It's counter intuitive, but looks correct.

 

OK, so I did accurate measurements on the location of my control arms.

Based on the formula, my front roll center is 13.3mm off the ground.

I am at 110mm ride height and have shorter than stock tires (225/45-15 Hoosier A6)

However, if I was to raise my ride height to LSS spec (120mm), my roll center would be lower = 10.5mm above ground. And at the base car ride height of 130mm, the roll center would be 7.3mm above ground.

This of course seems illogical. Lowering the car makes the roll center higher in this formula?? I don't see how that should be possible.

 

Yea I did not expect that result either. That was why I did some double checking but here is a bad (really bad) pic that might help. The left is the car at stock height and since the LCA is already point up towards the wheel as you lower it more it point way up so the green lines are the control arm projections and the yellow is the line you draw to the opposite wheel. so as its slope increases it raises the height of that intersect point and the roll center.

 

Also if you look in the spreadsheet m1 is the slop of the lower control arm m2 the slope of the upper y2 is the y intercept of the upper (the lower I defined to intersect thru the origin. And I think the rest you can pick off the diagram.

 

Since the lower control arm is higher at the balljoint than the chassis pivot, and the upper control is essentially flat, the lines intersect outside the plane of the car, correct?

So a line drawn from that intersection point to the middle of the tire doesn't pass through the middle of the car. So I am not sure how it calculates the roll center in the middle.

The control arm angles seem odd.

 

The first part you said is correct,
but that projected line can go thru the car. The roll center which is just a point in space could be on the inside of the car. If you look at some of the variables on the sheet like h, see how high it gets, and L how far away you have to project before the upper and lower control arm lines intersect. If those lines are intersecting really high, like higher than the height of the car (because they both pointed up) you will defiantly have to draw a line thru the car to the tire on the opposite side. Usually I don't think this would happen but our cars so low to the ground I guess it's possible.